La seconda legge di Gay-Lussac (legge isocora)
La seconda legge di Gay-Lussac (nota anche come legge isocora) dice che, a volume costante, il rapporto tra la pressione e la temperatura assoluta di un gas è costante:
\frac{p}{T}=kPer capire bene questa legge, immaginiamo di avere un gas con una pressione di 6 atm e una temperatura di 300 K (la temperatura assoluta viene infatti espressa in Kelvin e non in gradi Celsius). Se scaldiamo il gas e raddoppiamo la sua temperatura, la sua pressione raddoppia. Se lo scaldiamo ulteriormente e triplichiamo la sua temperatura, la sua pressione triplica; e così via. In altre parole, l’aumento della temperatura è direttamente proporzionale all’aumento della pressione, per cui il loro rapporto rimane sempre uguale:
\frac{6}{300}=0,02\frac{12}{600}=0,02\frac{18}{900}=0,02Perché ciò avvenga, è necessario che il volume rimanga costante (ecco perché la legge è chiamata anche “isocora”). Inoltre, il gas non deve essere troppo compresso e la sua temperatura deve essere lontana dalla temperatura di liquefazione.
Che cosa succede alle particelle del gas?
Per capire come mai la pressione sia direttamente proporzionale alla temperatura, dobbiamo osservare da vicino le particelle del gas. Infatti, in base alla teoria cinetico-molecolare sappiamo che il comportamento macroscopico di un gas dipende dal suo comportamento microscopico (cioè che la temperatura, la pressione e il volume di un gas sono variabili legate al comportamento delle sue particelle).
Quando il gas ha una certa pressione (p1) e una certa temperatura (T1), le sue particelle urtano le pareti del recipiente circostante con una certa frequenza. Se raddoppiamo la temperatura (T2), la velocità delle particelle raddoppia. A questo punto, se il volume non cambia (cioè se lo spazio in cui si muovono le particelle rimane lo stesso), è inevitabile che raddoppi anche la pressione, perché la frequenza degli urti raddoppia, essendo raddoppiata la velocità delle particelle.
La seguente immagine può aiutare a capire meglio ciò che avviene a livello microscopico:
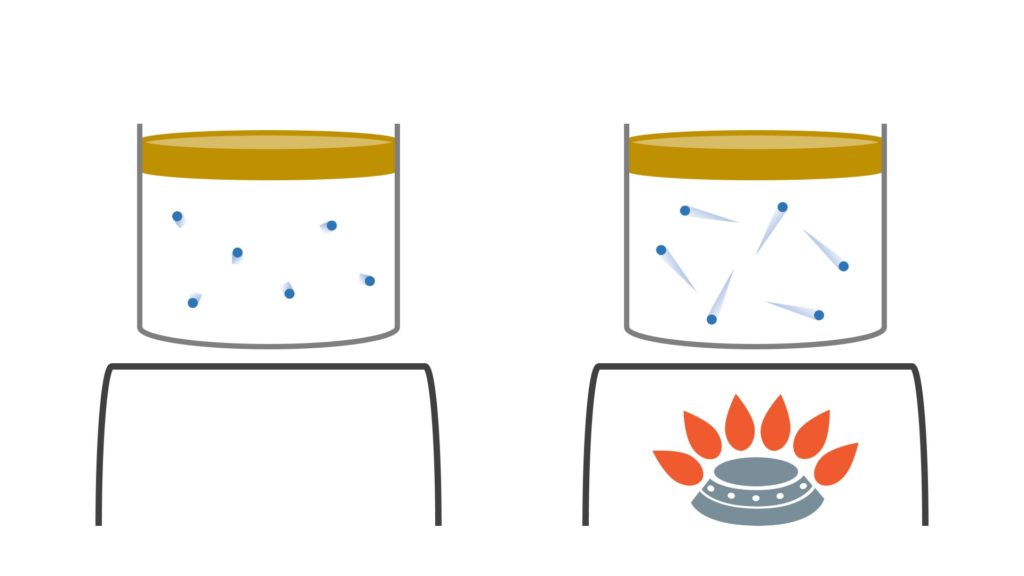
A mano a mano che scaldiamo il gas all’interno del recipiente, le particelle si muovono a velocità sempre maggiore, incrementando così gli urti contro le pareti circostanti.
Se però allargassimo il recipiente (cioè se facessimo aumentare il volume del gas), la pressione non aumenterebbe, perché le particelle avrebbero a disposizione uno spazio maggiore per muoversi e di conseguenza urterebbero le pareti con la stessa frequenza di prima.
Rappresentazione grafica
Questa correlazione tra la temperatura e la pressione di un gas corrisponde graficamente a una retta passante per l’origine:
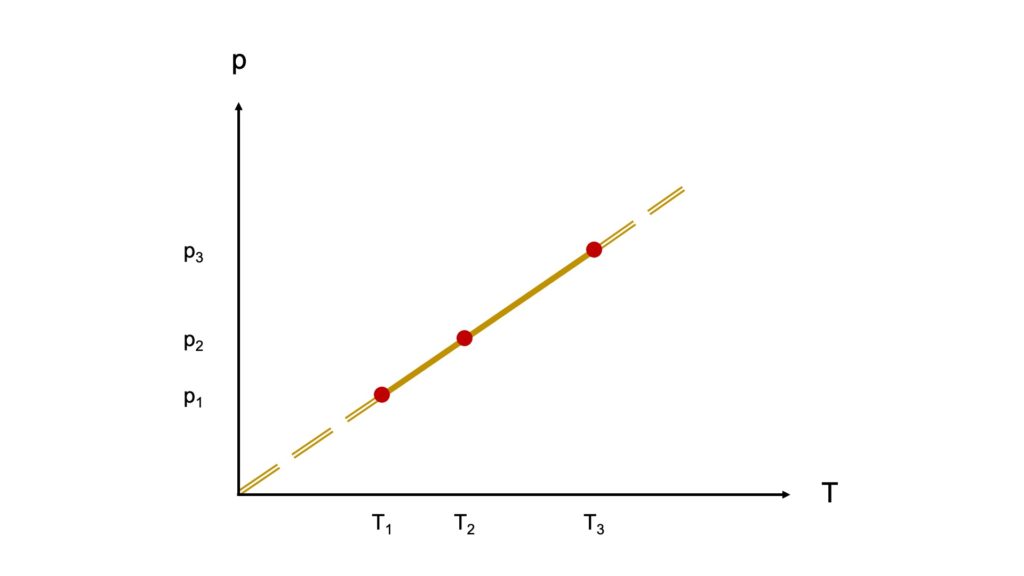
Come possiamo notare, all’aumentare della temperatura si verifica un aumento della pressione (e viceversa). Ciò vale per tutti i gas, dato che la seconda legge di Gay-Lussac è una delle leggi dei gas ed è quindi applicabile a tutti i gas (assumendo che i gas si comportino come un gas ideale).
Facciamo un esempio pratico usando i seguenti valori:
| p1 | = | 4 atm |
| T1 | = | 320 K |
| p2 | = | 4,5 atm |
| T2 | = | 360 K |
| p3 | = | 4,75 atm |
| T3 | = | 380 K |
In tutti questi casi il rapporto tra pressione e temperatura, che aumentano proporzionalmente, rimane sempre uguale. Possiamo pertanto scrivere:
\frac{p_1}{T_1}=\frac{p_2}{T_2}=\frac{p_3}{T_3}=kE quindi:
\frac{4}{320}=\frac{4,5}{360}=\frac{4,75}{380}=0,0125Rapporto tra pressione e temperatura in gradi Celsius
Come abbiamo visto, la seconda legge di Gay-Lussac stabilisce una correlazione tra la pressione di un gas e la sua temperatura assoluta. Questa correlazione non funziona tuttavia in maniera analoga con la temperatura in gradi Celsius, il cui aumento non comporta un aumento direttamente proporzionale della pressione.
Se ad esempio passassimo da 30° (= 303 K) a 60° (= 333 K), cioè se la temperatura in gradi Celsius raddoppiasse, non raddoppierebbe anche la pressione, perché non ci sarebbe un raddoppiamento della temperatura assoluta, che passerebbe infatti da 303 K a 333 K.
Il rapporto la pressione e la temperatura in gradi Celsius è basato sulla variazione di un singolo grado. A ogni aumento di 1° corrisponde infatti un aumento della pressione pari a 1/273 della pressione che il gas presenterebbe a 0° (ovviamente solo se il volume rimane costante).
La formula che esprime tale rapporto è la seguente:
p_t=p_0\ ·(1+\alpha\ ·t)
Dove:
- pt è la pressione del gas a una determinata temperatura (°C)
- p0 è la pressione del gas a 0°
- α è il coefficiente di espansione pari a 1/273
- t è la temperatura (°C)
La formula può quindi essere scritta anche in questo modo:
p_t=p_0+\frac{1}{273}\ ·p_0\ ·tCalcolare pressione e temperatura con la seconda legge di Gay-Lussac
Se la pressione (p1) e la temperatura (T1) di un gas a un certo punto cambiano, come facciamo a sapere quanto misura la sua nuova pressione (p2), conoscendo la sua nuova temperatura (T2) e presupponendo che il volume rimanga costante? Per rispondere a questa domanda, è sufficiente fare una semplice proporzione:
p1 : T1 = p2 : T2
Ad esempio:
| p1 | = | 5 atm |
| T1 | = | 320 K |
| p2 | = | x |
| T2 | = | 370 K |
A questo punto facciamo la proporzione:
5 : 320 = x : 370
Per cui:
x=\frac{5\ ·370}{320}=5,78\ atmE se la temperatura fosse in gradi Celsius? In questo caso non dobbiamo fare altro che sommare ad essa 273,15:
20° = 293,15 K
In questo caso le cifre decimali di solito vengono approssimate (e quindi 293,15 diventerebbe ad esempio 293).
