L’equazione di Van der Waals
L’equazione di stato dei gas ideali non è in grado di descrivere accuratamente il comportamento di un gas reale, perché un gas reale si comporta come un gas ideale solo ad alta temperatura e a bassa pressione (in caso contrario, il comportamento dei gas reali non rispecchia del tutto il modello dei gas ideali).
Al suo posto dobbiamo usare l’equazione di Van der Waals, un’estensione dell’equazione di stato dei gas ideali che tiene conto delle forze intermolecolari e del volume molecolare del gas preso in esame (e che quindi descrive con maggiore precisione il comportamento dei gas reali):
\left( p+\frac{n^2\ ·a}{V^2} \right)·(V-n\ ·b)=n\ ·R\ ·TCome possiamo notare, l’equazione di Van der Waals si basa proprio sull’equazione di stato dei gas ideali:
p\ ·V=n\ ·R\ ·T
Tuttavia, la pressione (p) e il volume (V) sono stati ricalcolati. In un gas reale infatti:
- le forze intermolecolari non sono nulle, per cui alla pressione bisogna aggiungere la pressione interna generata dall’attrazione tra le molecole
- il volume molecolare non è nullo, per cui al volume bisogna togliere il volume occupato dalle molecole
Vediamo in che modo la pressione e il volume sono stati ricalcolati:
Pressione
In un gas reale le molecole si attraggono reciprocamente in ogni direzione, ma a ridosso delle pareti del recipiente questa attrazione si verifica solo da un lato (dall’altra parte c’è infatti la superficie del recipiente):
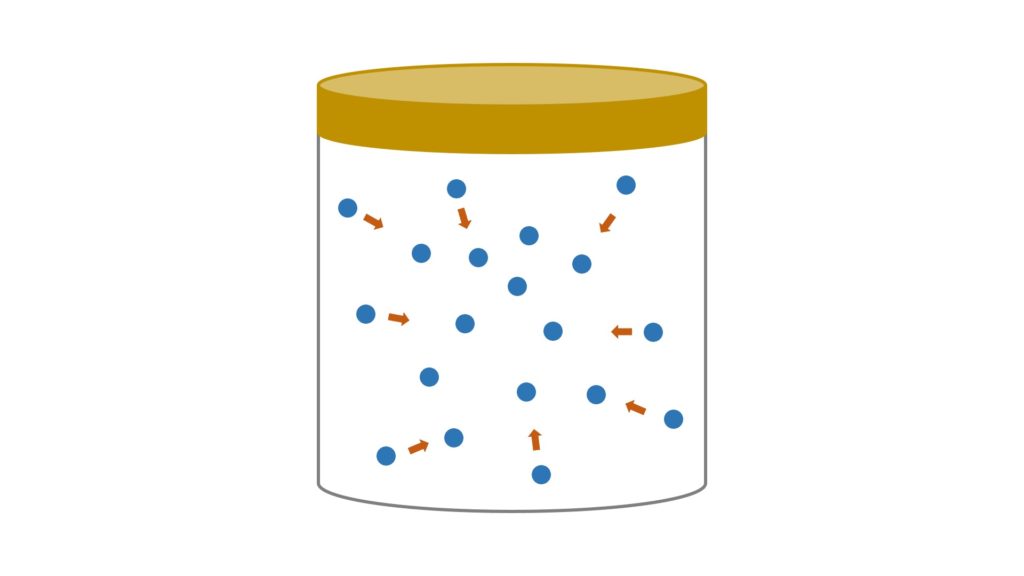
Si crea così una pressione interna che prende il nome di pressione di coesione, una sorta di forza che punta verso il centro. Poiché questa pressione è legata all’attrazione delle molecole, essa è proporzionale alla densità del gas (cioè alla concentrazione delle molecole) elevata al quadrato. Perché elevata al quadrato? Perché ogni molecola, allo stesso tempo, attrae ed è attratta (in pratica, è come se dovessimo considerare la densità sia delle molecole che attraggono sia delle molecole che sono attratte, cioè la medesima densità moltiplicata per se stessa):
\frac{n^2}{V^2}Dove:
| n | = | numero di moli |
| V | = | volume |
Inoltre, dato che in ogni gas l’intensità del legame tra le molecole è diverso, dobbiamo moltiplicare la densità al quadrato per il coefficiente a, un valore sperimentale diverso per ogni gas che ci permette di tenere conto di quanto intensamente si attraggono le molecole (e non solo del fatto che esse si attraggono). Otteniamo così la pressione di coesione:
a\ ·\frac{n^2}{V^2}Se a questo punto sommiamo la pressione del gas alla pressione di coesione, otteniamo la formula che compare nell’equazione di Van der Waals:
p+\frac{n^2\ ·a}{V^2}Volume
In un gas reale il volume che le molecole hanno a disposizione per muoversi liberamente non è il volume totale del recipiente, ma la differenza tra il volume totale del recipiente e il volume materialmente occupato dalle molecole.
Dato che in ogni gas le dimensioni delle molecole sono diverse, il volume che dobbiamo togliere è pari al numero di moli del gas (cioè l’insieme di tutte le sue molecole) per il coefficiente b, chiamato anche covolume (o volume escluso), un valore sperimentale diverso per ogni gas che ci permette di tenere conto di quanto sono grandi le molecole del gas preso in esame:
V-n\ ·b
Dove:
| V | = | volume totale del recipiente |
| n | = | numero di moli |
| b | = | covolume |
Elenco dei coefficienti
Ecco l’elenco dei valori dei coefficienti a e b per i principali gas (in fondo all’elenco ci sono le unità di misura di entrambi i coefficienti):
| Gas | a | b |
| Acido solfidrico (H2S) | 4,4 | 0,043 |
| Ammoniaca (NH3) | 4,0 | 0,036 |
| Anidride carbonica (CO2) | 3,60 | 0,043 |
| Argon (Ar) | 1,345 | 0,032 |
| Azoto (N2) | 1,40 | 0,039 |
| Elio (He) | 0,034 | 0,024 |
| Etilene (C2H4) | 4,4 | 0,056 |
| Idrogeno (H2) | 0,25 | 0,027 |
| Metano (CH4) | 2,25 | 0,043 |
| Neon (Ne) | 0,217 | 0,027 |
| Ossigeno (O2) | 1,39 | 0,032 |
L’unità di misura di a è:
\frac{atm\ ·L^2}{mol^2}L’unità di misura di b è:
\frac{L}{mol}Dove:
| atm | = | atmosfere |
| L | = | litri |
| mol | = | moli |
